Editor’s note: In the past few weeks, have you wondered what it would be like riding along with Rosetta, sitting on top and watching comet 67P/C-G drawing steadily closer? And what if, as a Rosetta-riding-astronaut, you got right up close to the mysterious object, near enough to reach out and touch it? In fact, if you were standing on Rosetta, which, ignoring the huge solar arrays, is basically a box 3X2X2m (about the size of a small garden shed), could you get near to the comet, leap off the spacecraft and actually land on 67P? Hmmm… Now that would be cool! As usual with such tough questions, we turned to Professor Rhett Allain and asked him to think this one through for us.
Rhett Allain
Dr Rhett Allain is Associate Professor of Physics at Southeastern Louisiana University. He writes regularly for Wired’s Dot Physics blog and (like most of us working on Rosetta) is a bit of a physics fanatic. He is author of “National Geographic Angry Birds Furious Forces: The Physics at Play in the World’s Most Popular Game.” He has contributed guest posts to ESA’s ATV blog, including: Could we use ATV to build and supply a real Death Star? Using astronaut Mike Fossum’s YouTube video to measure ATV acceleration and How many calories does it take to bring a calorie to the ISS? (The link to this last one got tweeted by @NASA when we posted it in 2013, and the resulting traffic broke our server… but that’s another story.)
Guest post by R. Allain
It’s almost there. The Rosetta spacecraft will soon rendezvous with comet 67P/Churyumov-Gerasimenko
Could an astronaut just jump onto the comet?
Suppose that an astronaut was riding along with the spacecraft Rosetta. If Rosetta made a close pass to the comet (which it will), could the astronaut just jump off and land on the comet? It would be just like a cowboy jumping from a horse to a train – if it could work. Let’s get started.
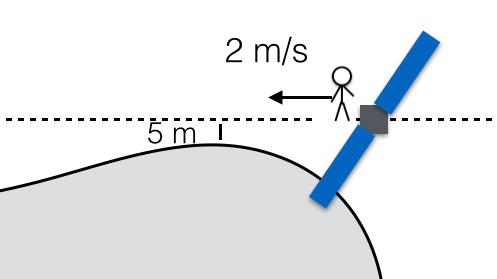
Here is how this could be set up. Suppose that Rosetta makes a close pass to the comet with a speed of about 2 m/s relative to the comet and at closest approach it is about 5 meters away.
Of course that sketch isn’t to scale, but it gives you an idea of what would happen. You might also ask, “Why is there an astronaut on that spacecraft?” Why would you ask such a crazy question? Clearly, the astronaut wants to get off the spacecraft on onto the comet.
Here are some other starting assumptions.
- Comet 67P has a mass of 3.14 x 10E12 kg and a radius of 2 kilometers; of course it isn’t spherical – but let’s assume it’s spherical also.
- During this jump-off time, the Rosetta spacecraft mostly moves in a straight line until the astronaut jumps off.
- Rosetta has a mass of 1580 kg (including the remaining fuel and the 100 kg lander).
- The astronaut has a mass of 80 kg (human-plus-space suit).
- The gravitational force from the Sun is nearly constant at this location. I think this is a pretty safe assumption.
- The acceleration of the comet due to its orbital motion is also small. This means that in the comet reference frame, I can ignore the fake forces of centrifugal force and Coriolis force.
That’s enough data to start with. Let’s break this motion into different parts.
The jump
The astronaut has to jump in order to try to match the velocity of the comet. In the comet reference frame, the comet is stationary and the spacecraft moving at 2 m/s. Could the astronaut jump such that the astronaut ends up with a zero m/s speed?
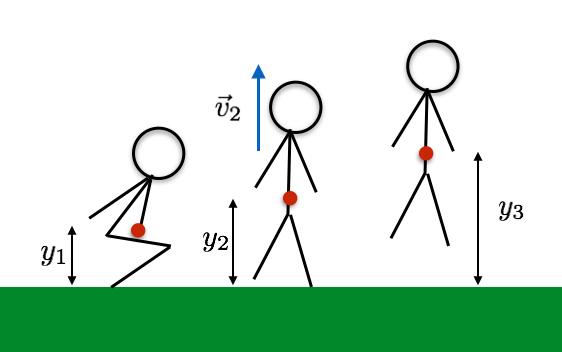
How hard can an astronaut jump? I’m just thinking about a typical human here – not a professional athlete. On the surface of Earth, let’s say this astronaut could jump in a way to gain a height of 20 cm. Note that is the change in height of the center of mass and not how high the feet move (you could pull your feet up to get more clearance but your center of mass would still only change by 20 cm).
During this process, the astronaut goes from a center of mass of y1 to y2 while pushing on the ground and speeding up. At point y2, the astronaut no longer continues to push on the ground. However, there is some velocity and the astronaut continues to move upwards.
All we really need is the work done by the astronaut during this jump. That means that I need the distance the astronaut bends down while jumping. Let me estimate these three heights as 75 cm, 103 cm and then 123 cm. Since the astronaut starts at position 1 with a velocity of zero and ends at position 3 with a velocity of zero, the work required from the astronaut would just be equal to the change in gravitational potential energy. An 80 kg astronaut jumping a total height of 0.48 meters would require 376.3 Joules (assuming the work done by gravity is m*g*h).
It isn’t really needed right now, but we can also calculate the ‘launch speed’ as the astronaut leaves the ground. In order to move up 20 cm in height, the astronaut would have to start with an initial speed of 1.98 m/s.
Now for the assumption. Let’s assume that when the astronaut jumps off Rosetta, the same amount of energy is used. Of course this might not actually be true, but it’s a good place to start.
Jumping off a spacecraft
If an astronaut can jump on the surface of the Earth with a speed of 1.98 m/s, couldn’t the astronaut leave the spacecraft with the same speed? Maybe not. There is something very different about jumping off the spacecraft and jumping on the Earth – the spacecraft will move away as the astronaut jumps.
Here is a diagram both during and after the “jump’.
As the astronaut pushes on Rosetta, Rosetta pushes back with the same force (this is the basic nature of forces). Also, the force on the astronaut and the force on Rosetta act for the exact same time (since it is the same interaction). The momentum principle says that a force multiplied by a time interval gives you the change in momentum of that object. This means that after the ‘push’, Rosetta and the astronaut will have equal and opposite momentums.
So we now know two things. We know that the momentum (magnitude of momentum) of the astronaut and Rosetta will be the same and we know the total kinetic energy of the two objects (the 376.3 Joules from jumping). I can write this as:
Note that I sort of cheated. First, I wrote the equations for just the magnitudes of the velocities. Second, I assumed that both Rosetta and the astronaut were at rest before the push. Trust me. Everything will be ok in the end. Oh, notice that I am calling the work the astronaut can do Wa.
The nice part is that now I have two equations with two unknowns (the two final velocities). Using some algebra, I get the following two speeds:
Just a quick check. What if Rosetta is the Earth? As the mass of Rosetta gets huge, you can see that it has essentially zero recoil speed and all of the energy goes into the jumping astronaut. It’s always good to check these things.
Putting in values for the masses and the work done by the astronaut, the astronaut would ‘jump’ at a speed of 2.99 m/s and Rosetta would recoil at 0.15 m/s.
But wait! How is this possible? The astronaut had a greater jumping speed when the spacecraft recoiled than on Earth. Is that crazy? It’s only partly crazy. When the astronaut jumps on Earth, the astronaut does two things: he or she works against gravity and increases his or her kinetic energy. When jumping off Rosetta, the gravitational force between the astronaut and Rosetta is super small. If this makes you feel better, if Rosetta was very massive and all of the kinetic energy went to the astronaut, the astronaut would have a jumping speed of 3.07 m/s.
Could the astronaut jump to the comet?
Yes. It seems that this could work. As Rosetta passes by the comet at a speed of around 2 m/s, the astronaut jumps off the spacecraft. Since the jumping speed could be over 2 m/s, the astronaut could jump in a way so as to be essentially stationary with respect to the comet.
Would an astronaut ”fall’ onto the comet?
Let’s say the comet has a mass of 3.14 x 10E12 kg and a radius of 2 km (as stated previously). We can calculate the gravitational force between the astronaut and the comet using the gravitational force equation:
Where r is the distance from the center of the comet to the astronaut and G is the gravitational constant. Putting in values for the mass and radius of the comet, I get a gravitational force of 0.0042 N and a free-fall acceleration of 5.24 x 10E-5 m/s2. Since the distance doesn’t change too much as the astronaut ‘falls’ (5 meters out of 2,000 meters), this acceleration would be constant.
How long would it take an astronaut to fall to the surface from a height of 5 meters? For objects with constant acceleration, I can use the following kinematic equation:
I know that the change in y is -5 meters and that the initial y-velocity is 0 m/s. This makes it easy to solve for the time:
Using the acceleration from above and a height of 5 meters, I get a free-fall time of 436.9 seconds (7.3 minutes). That’s a long free fall! Enough time to watch a couple of YouTube videos.
So the answer is: Yes. A human astronaut could probably just jump off a spacecraft and land on a comet. Now we just need to do it!
Note: Keen on more Rosetta physics challenges? Read Rhett’s dotphysics blog post: Rosetta Meets a Comet and You Get Homework
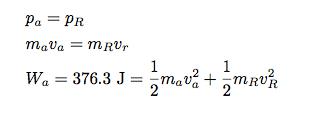
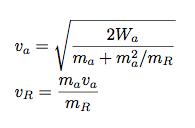
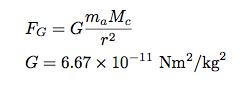
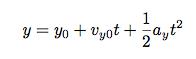
Discussion: 15 comments
I’m a volunteer to do this jump. 🙂
But would the astronaut simply bounce off again, in the absence of some kind of tethering mechanism, such as a harpoon?
I’m most appreciative of this blog entry with the math concepts included – I feel challenged to get out of my proverbial armchair and dust off my old A-level textbooks. Keep it up pls. – ESA you’re doing great with all these topical blogs, timed to perfection.
May I respectfully ask that in due course the Philea landing attempt will also be explained with some math to let us try and look over the shoulders of the navigators?
Is this kind of the same calculation they will use to place the rosetta lander on the surface? They will eject it with the right force so it will have the speed of the passing by comet and let it softly glide down by the gravitatonal pull of the comet to its surface? So the whole landing will take may be 10 hours if they eject it form lets say 1 km distance?
Apparently there are two launching mechanisms for the lander: the primary has a variable mechanism and the back up is a non variable but higher force mechanism, in case the primary doesn’t work (lets hope not!). Essentially the lander is to fall under gravity to the comet’s surface with no further attitude or directional adjustments possible, either from earth or the lander itself. So in selecting sites for the lander, ESA have to come up with 2 one for the primary mechanism and another for the secondary mechanism and both have to have the right characteristics- good sunlight smooth landing site etc .
Lets all hope that after 10 years in space all goes well- it would be a disaster should Philae tumble on its way to the surface.
…assuming v_r = v_R.
Thoughts of the astronaut:
“My impact velocity will be
v = a x t = 5.24 x 10E-5 m/s2 x 436.9 s = 0.01857 m/s.
Oh no, that comet is rotating once every 12.4 hours, so the velocity at the equator is
U / T = 2 x pi x r = 2 x pi x 2000 m / (12.4 x 3600 s) = 0.2815 m/s.
I should have taken this into account before jumping right over the equator.
So my impact angle is a mere
arctan(0.01857 m/s / 0.2815 m/s) = 3.77°.
Fortuantely the escape velocity of the nucleus is
v_e = sqrt(2GM/r) = sqrt(2 x 6.67x10E-11 Nm2/kg2 x 3.14 x 10E12 kg / 2000 m) = 0.4576 m/s.
But wait, the velocity for a circular orbit is just
v_circ = v_e / sqrt(2) = 0.4576 m/s / sqrt(2) = 0.324 m/s.
So I’ve to take care not to walk faster than 0.042 m/s in the direction of rotation. And no elastic bouncing … please.”
Yes. And I would assume that the same apply to jet fighter pilots 🙂
WIth Regards
TJ
Good old ROS the Fastronaut. His Pa is with the Pros
This is so over my head that Rosetta is closer but just so cool even just to read it. thank you all. Reading these blogs gives it all life.
The hardest step, training to hold your breath for ten years.
Now, do the calculations for the actual orbital distance of some fifty kilometers.
Also it’s not clear at all if 2 m/s is a realistic relative speed.
There ´s a problem when astronaut jump off from Rosetta 67P doesn’t have enought attraction and astronaut lost in Space
With the gravitational pull increasing 25-fold as Philae descends from (?) 10km to 2km, the equations of motion are more complex.
Simulation on a spreadsheet is ok but I wonder if there is an algebraic expression solving the equation x” = -k/x^2.
If landing speed is to be 1m/s, fall-time is > 10k” (~3hrs) and 7 hr (25k”) has been indicated.
Is the aim to land vertically, matching comet surface speed (0.2m/s?) or not. 0.2*25k” is still a 5km offset from the vertical.
It seems to be an extraordinary achievement to land on the comet at all, let alone land tolerably near the bullseye. Respect!
g
If Rosetta were in circular free orbit as close as safe to 67p, what orbital period and speed would it have. I can foresee a “3 body problem” because the two dumbell parts have diverging gravity field components when attracting a spacecraft so near.