By Rhett Allain
If the International Space Station (ISS) orbits at an altitude of about 410 km above the Earth, why does it sometimes take a vessel like ATV two days – or more – of travelling to get there? If you drove your car 410 km at highway speeds, it would only take about 4 hours. So why does a spacecraft with pretty powerful rocket engine take so long? The answer is that it’s all about orbital mechanics.

ATV-4 “Albert Einstein” Lego(TM) model. Image copyright & credit: Stefan Schindler Via Flickr
Editor’s note: In addition to having a knack for science communication, Rhett Allain is Associate Professor of Physics at Southeastern Louisiana University. He writes regularly for Wired’s Dot Physics blog and is a bit of a physics fanatic who spends more time than many pondering how daily life intersects with science. With the recently announced development of ATV in cooperation with NASA for Orion, we’re delighted to feature a few posts from the far side of the Atlantic. Enjoy!
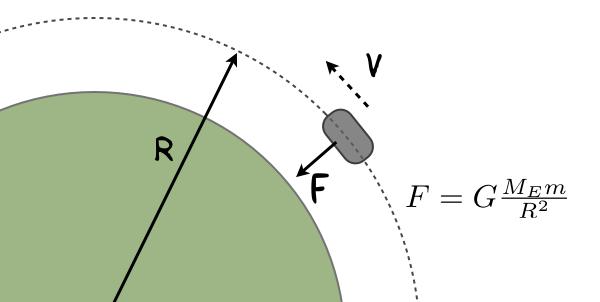
Suppose you, like ESA, want a spacecraft to orbit the Earth in a circular path. Below is a sketch of that object with the only force acting on it (note that this is not to correct scale). There is just one force on this object, the gravitational force from the interaction with the Earth.
The thing that is the most important here is the R2 on the bottom of the equation. This says that as you get farther away from the center of the Earth, the gravitational force decreases. Well, that’s all fine and dandy, but why does that matter? Just hold on and you will see.
[Editor’s note: Before reading any further, it may be fun to quickly glance at our earlier post ‘ATV-4: Ten days launch to docking‘ – an explanation why it takes so long to dock written before Dr Rhett sent in his analysis below. Also, we’ve included a comment from the ATV flight dynamics team at the end of Rhett’s post – Ed.]
There is another important thing to consider. What does a force do to an object? The correct answer is that it changes the velocity of that object (if you said that it changes the momentum, that would be an acceptable answer also).
Now, instead of just writing something like F = ma, let me make another important point. Acceleration doesn’t just mean something is changing speed. When an object changes direction, that is an acceleration also. The magnitude of the acceleration of an object moving in a circular path depends both on its speed and the radius of the circle it is following. So, for an object moving in a circle, I can write:
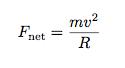 But sometimes we like to think of circular motion in terms of the angular velocity of the object instead of the linear velocity. That would make the force equation a little different. This will be useful later.
But sometimes we like to think of circular motion in terms of the angular velocity of the object instead of the linear velocity. That would make the force equation a little different. This will be useful later.
![]() Now we can put this all together. We know that both the force and the acceleration depends on R.
Now we can put this all together. We know that both the force and the acceleration depends on R.
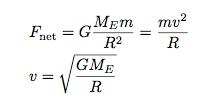 This says that in order to be in a circular orbit around the Earth, the object must have a certain speed. And if you want to orbit at a higher altitude, the object wouldn’t have to go as fast.
This says that in order to be in a circular orbit around the Earth, the object must have a certain speed. And if you want to orbit at a higher altitude, the object wouldn’t have to go as fast.
But how can you ‘catch up’ to another orbiting object? [Like the ATV catches up to the ISS? – Ed.] One simple solution is to be in a lower orbit. What if you were watching the two orbiting objects from the surface of the Earth? In this case you would say that the ‘catching up’ object needs to have a greater angular speed.
If I solve for the required angular speed in orbit, I get:
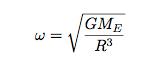 Now, using this I can put in the parameters for the ISS at an altitude of 410 km; this gives an angular speed of 1.1288 x 10-3 radians/second (rad/s). Let’s suppose the ATV is trying to catch up at an altitude of 300 km. This would give it an angular orbital speed of 1.1568 x 10-3 rad/s. That’s just a little bit faster than the ISS. So then, when would these two object have the same angular position? Of course, that depends on how far back the ATV starts.
Now, using this I can put in the parameters for the ISS at an altitude of 410 km; this gives an angular speed of 1.1288 x 10-3 radians/second (rad/s). Let’s suppose the ATV is trying to catch up at an altitude of 300 km. This would give it an angular orbital speed of 1.1568 x 10-3 rad/s. That’s just a little bit faster than the ISS. So then, when would these two object have the same angular position? Of course, that depends on how far back the ATV starts.
Suppose the ATV starts a distance back about the same as the distance from Los Angeles to New York City – about 4,500 km. At the ISS orbital altitude, this would be an angular distance of 0.663 radians. Now I can just solve for the time it takes the two objects to have the same angle. I will assume the ISS starts at an angular position of 0.0 radians.
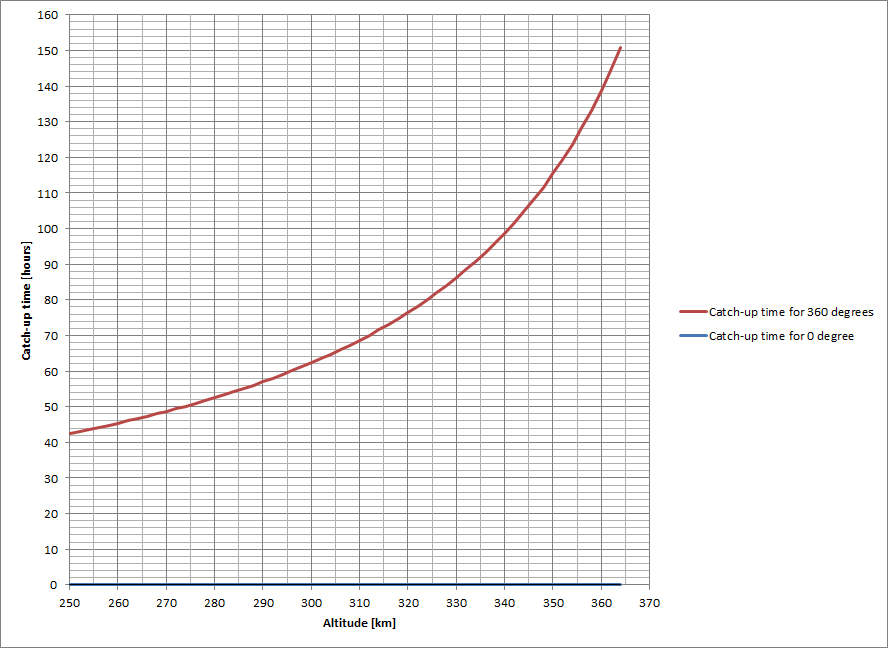
Using the above values for the angular speeds, I get a catch up time of 394 minutes. What if the ATV is at an even lower orbit? Well, then it would take less time to catch up, of course. Let’s just plot the catch up time for different starting altitudes.
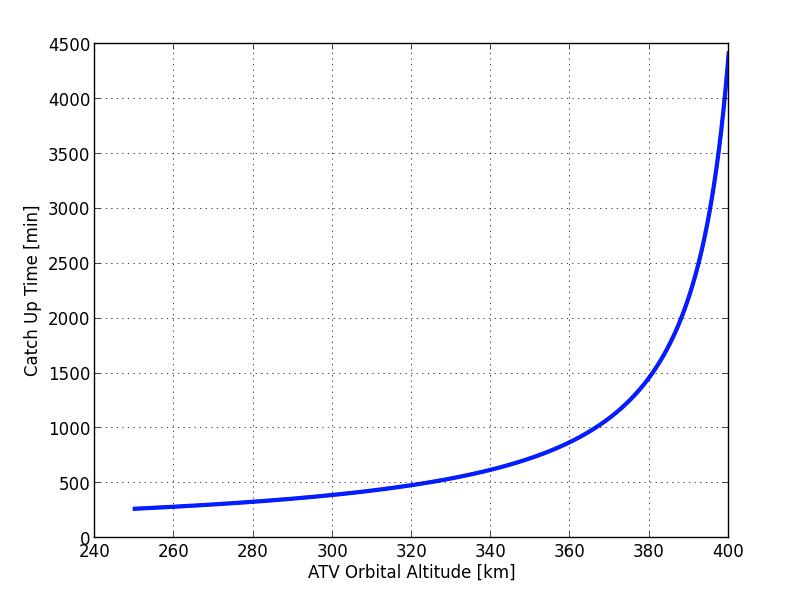 So, the closer in altitude the ATV is to the ISS, the longer it will take to catch up. But what does all this mean for ATV’s orbital rendezvous with the ISS? It means two things: First, you can’t just zoom up to the ISS. Second, orbital mechanics can be quite complicated!
So, the closer in altitude the ATV is to the ISS, the longer it will take to catch up. But what does all this mean for ATV’s orbital rendezvous with the ISS? It means two things: First, you can’t just zoom up to the ISS. Second, orbital mechanics can be quite complicated!
|
Follow-on comment provided by ESA’s ATV flight dynamics team In this (excellent) post, Dr Rhett used an example of 4,500 km – a distance equivalent to 0.663 radians. If this angular distance were 360 degrees, then the calculation above would yield ~62 hours to ISS rendezvous for a vehicle drifting in free-flight orbit at 300km altitude. Assuming that the angle to catch-up with the ISS is between 0 and 360 degrees, the catch-up time will be between the two curves below: So, while some vehicles can rendezvous with the ISS in just a few hours, ATV takes five days.
|
Thank you to Rhett Allain and to Laurent Arzel and Nathalie Vedie at ATV-CC.

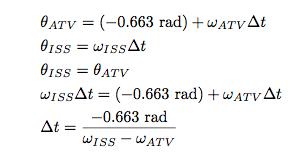
 Automated Transfer Vehicle page
Automated Transfer Vehicle page ATV blog archive
ATV blog archive
Discussion: 4 comments
I have been reading about the new flight profile of the progress MS-08 launching this month that would take only 3 hours.
I was searching for more in depth information and this article was very useful.
Hopefully other vehicles can also be upgraded to the 3 hour rendezvous, specially crewed vehicles such as the crewed dragon.
So why does it take so long to reach the ISS? After all, once you’re already in space, the ISS is only miles away. And Earth’s gravitational pull is weak, which means a little power can take you a long way.
Hello Justin, thank you for your reply. If you could explain in a little more detail from the point where Mr.Allain
states: If I solve for the required angular speed in orbit, I get..how the angular speed was dervied and what brought the time calculation to end up at 397 minutes. Fascinating material.
Thank you,
Jayson David
So, how do you determine the angular velocity for a circular orbit? Here is a short explanation. Hopefully this helps.
https://youtu.be/nQ9ENxoHrDQ