How to determine the orbit of a comet?

In movies about the impending end of the world due to a comet impact, one thing is certain: Detecting the comet and computing its orbit are dead easy. The scene starts with a computer screen showing a telescope image of a star field, where we can make out a faint, fuzzy little object that doesn’t quite look as if it belonged there.

Control room at ESA’s Optical Ground Station Credit: ESA

A scientist will throw a brief, disinterested glance at the screen and turn away. Then he stops. His eyes go wide and he snaps around to stare at the screen. He’ll call in his colleagues. Computer programs are started, and people frantically hack away at keyboards. In no time at all, they will have identified the fuzzy blob as a comet that is hurtling in from the frozen recesses of space.

Better call this guy!

What’s more, in no time at all, they will have determined the comet’s trajectory and they can categorically state that it will hit Earth. A few more frantic calculations and they also know the date and time of impact – Quick, call Bruce Willis!

Neat. But does it really work like that?

In actual fact, one single picture of a comet is just that: a single picture of a comet. All this picture tells you is that there is a comet which, at a certain date and time – a certain epoch (astronomers like to use common words with meanings that are just different enough from what you think the word means to create confusion, so they say ‘epoch’) – appeared to be near stars A, B, and C in constellation X. No more.

From one picture, you can’t tell where it’s heading; you don’t know how close it will get to the Sun, nor if or when a close encounter with any other planet is due. To find out these things, you need more observations – many more of images that were taken at different dates, ideally spanning a long time frame. The longer the better.

There it is!

And even then, computing the orbit is not really a straightforward matter. In fact, it’s a drudgery and you have to go about it in a roundabout way. The pictures don’t tell you the comet’s path. All they do is to tell you where the comet appeared to be seen at the stated epochs from wherever the observatory was located. But that is not what you want to know.

So you have to make an educated guess at the parameters that describe the comet’s trajectory, also known – unsurprisingly – as its ‘orbital parameters’. This initial guess (as even the mathematicians rather candidly refer to it) in all likelihood will be quite far off. That’s OK, it’s just a guess. But at least, you have something to work with.

A famous mathematician

Once you have the initial guess, you have a set of orbital parameters that apply to a given reference epoch that you are free to choose. The known laws of celestial mechanics allow you, if you have a full set of orbital parameters at one epoch, to compute where the object will be at other epochs in the past or in the future. So you can compute where it would have been at the epochs when the comet images were taken. Because the Earth’s orbit is well known, you can then compute in which constellation and next to which stars the comet would have appeared at these epochs, assuming that your initial guess holds.

For the initial guess, you will probably find out that the locations in the sky that you compute for the image epochs are quite different from what the images show. Hardly surprising, given that that was just the initial guess. But then you can make small changes to each of the orbital parameters for the initial guess to see which change makes the computed locations at the image epochs move closer to the actually observed locations. At all times, you can use the very accurately known positions of the background stars to get your bearings.

This procedure is known as ‘orbit determination’.  It is very time-consuming and involves a lot of complicated and repetitive mathematical calculations, which is why nowadays we let a computer handle most of it. The entire process is known as ‘parametric optimisation’ and each step is referred to as an ‘iteration’. As the optimisation process goes on and many iterations have been performed, you will see that for the epochs at which the images were taken, the computed locations, based on the current estimate of the orbital parameters, will move quite close to what you can see in the actual images.

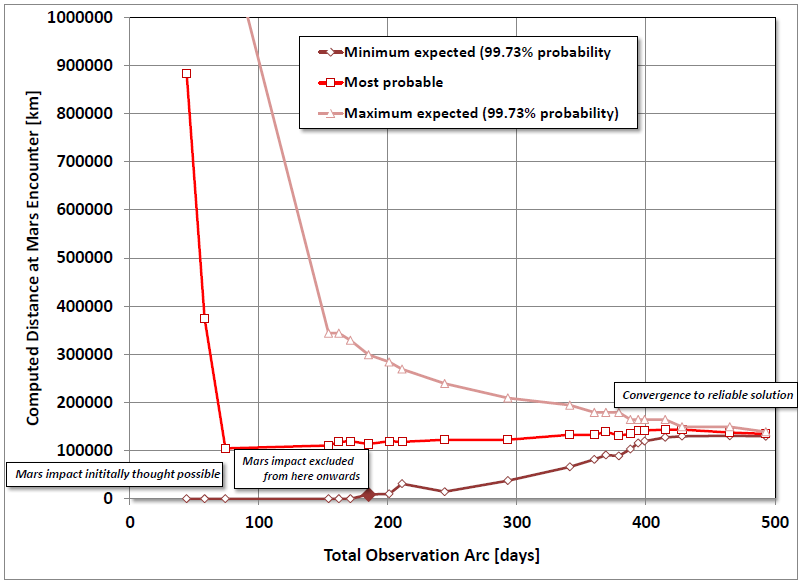
This diagram is indicative of how the orbit determination accuracy for comet C/2013 A1 (Siding Spring) evolved over time. It shows a derived quantity: the expected encounter distance from Mars. Source of data: NASA/JPL

At some point, there will be no further improvement. The process will have ‘converged’ in mathematicians’ parlance. But wait: this does not mean that you’re done. It just means that you can do no better with the available information, in this case, the available set of photographic images. There is always some uncertainty in measuring just where an object is with respect to the background stars. Comets appear fuzzy and blurred. Who’s to say what their exact position in the celestial vault is on that image you’re gazing at? Might it not be a few hundredths of a degree further up? But, on a cosmic scale, such minute differences matter – a lot!

Furthermore, if the time span between the earliest and the latest available image is short (just a few weeks or even a few days) the information they contain may be ambiguous. Comets on a wide variety of orbits might still appear to be in that location over a short period of time. But you will see that in the results of the orbit determination, because the mathematical process involved will not only give you a best estimate of the orbital parameters, it will also tell you how accurate (or inaccurate) that best estimate is.

The problem is that if you know the orbit only approximately at that reference epoch you selected at the start of the process, and you want to propagate ( i.e. compute the time change in the orbit, subject to the laws of celestial mechanics and any effects that may change the orbit) this orbit to another epoch, you will find that any uncertainty in the initial parameters will balloon, the further you propagate.

In the diagram above, it took almost 200 days to find out that comet Siding Spring would not hit Mars. At that time, the uncertainty in the predicted encounter distance still ran into hundreds of thousands of kilometres. Though the most probable encounter distance was established fairly early, the uncertainty was still significant after more than a year of observation. It took 44 days of observation to achieve even a semblance of an orbit determination – one that was still all over the place, with a predicted mean Mars distance at flyby 900,000 km, with a high guess of 3.6 million!

Sincere thanks to Michael Khan for today’s post – Ed.