Today’s post is contributed by Florian Renk and the Mission Analysis team at ESA’s ESOC operations centre, Darmstadt. Florian did a lot of the planning work to analyse the ‘hows’ and ‘whens’ of LISA Pathfinder’s trip to space.

On 3 December, a new mission joined ESA’s fleet of spacecraft around Earth. Well, in this case, it’s not exactly around Earth. Or is it?

LISA Pathfinder is travelling to an orbit around the so-called L1 Lagrange point, also called the Sun-Earth Libration Point 1. SEL1 is located about 1.5 million km toward the Sun from us, when looking at the Sun from the Earth. It lies in the ecliptic plane, the plane in which the Earth moves around the Sun, so like the Earth, the libration point also moves around the Sun, making a complete orbit in one year. While it’s just a point in space, it exists because the gravitational pull of the Sun and the Earth provide just the right centripetal force in this spot to rotate with them.

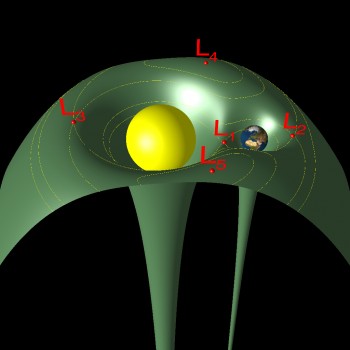
The surface indicates the effective potential created by the two massive bodies and the rotation of the secondary body around the primary. The libration points are located at the saddle points.

The surface indicates the effective potential created by the two massive bodies and the rotation of the secondary body around the primary. The libration points are located at the saddle points.

Compared to previous ESA spacecraft travelling to one of the Sun-Earth libration points (there are five), the journey of LISA Pathfinder is a bit more complicated. Herschel and Planck were launched on the powerful Ariane 5 rocket and Gaia got a smooth ride on the Soyuz-Fregat launcher. LISA Pathfinder, however, has started its journey to SEL1 on Europe’s smallest launcher, the Vega.

Europe’s launchers from Kourou: Vega, Soyuz-Fregat and two versions of the Ariane 5

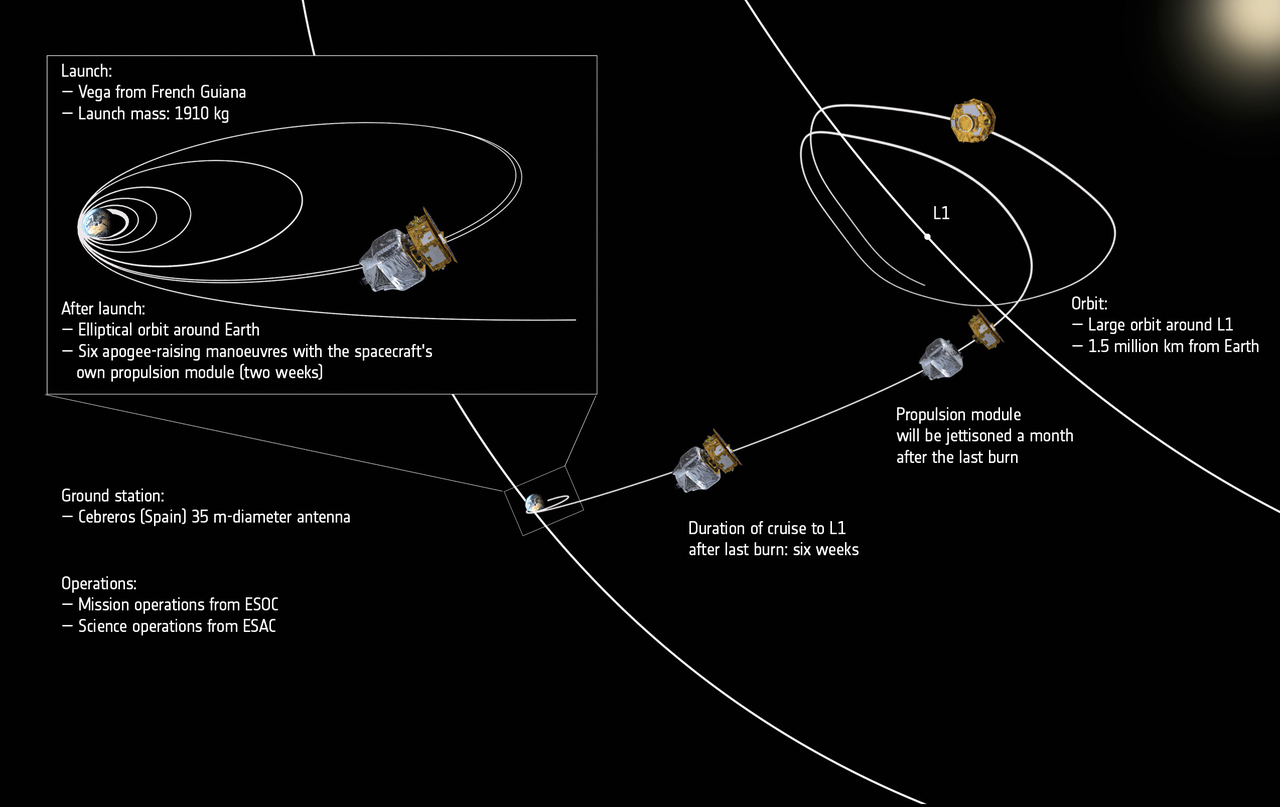
Vega is not powerful enough to directly propel LISA Pathfinder towards its destination at 1.5 million km from Earth. It can only provide the initial ride into space and delivered the spacecraft into a slightly elliptic Earth orbit with a perigee (the closest point to Earth) of about 200 km and the apogee (the furthest point from Earth) of about 1540 km.

Launchers at Europe's Spaceport Credit: ESA

Launchers at Europe’s Spaceport Credit: ESA

From this initial orbit, LISA Pathfinder must now use its own propulsion module to travel to SEL1. And this journey is a tricky one!

ARMs 1 to 6

To travel to SEL1, LISA Pathfinder must raise its apogee to be near the 1.5-million-km point and to do so the spacecraft will perform a sequence of ‘apogee raising manoeuvres’ (ARMs) providing a velocity increment of more than 3000 m/sec (in comparison, when Rosetta came out of deep-space hibernation in January of 2014 to start slowing down to catch comet 67P/C-G, it only had to slow its speed by 800 m/sec.).

Further, the apogee cannot be raised in just one ‘big burn’, since LISA Pathfinder would need an extremely large main engine to perform this manoeuvre. Instead the craft’s propulsion module is equipped with a 450-Newton main engine (which is still pretty big! Rosetta has 24 10N thrusters) and will conduct a series of six burns between 7 and 12 December.

Note: Additional thruster burns are planned to trim and correct the final trajectory; the six until mid-December are the biggies. Sometimes, spaceflight engineers say ‘manoeuvre’ when they mean ‘thruster burn’ or just ‘burn’ – these terms are all more or less equivalent wording.

To actually fire the main engine installed on LISA Pathfinder (actually, installed on a Propulsion Module attached to LPF, which will be jettisoned at the end of January), the mission control teams must adhere to some strict constraints.

One is the maximum burn duration the spacecraft can conduct; the burns usually take place in Earth eclipse (i.e. when the craft is in the darkness of Earth’s shadow) and thus we have to be careful with the available battery power. A single burn cannot run too long before the spacecraft must again be pointed toward the Sun to recharge its batteries.

LISA Pathfinder spacecraft after propulsion module has been discarded Credit: ESA

LISA Pathfinder spacecraft after propulsion module has been discarded Credit: ESA

After each burn, we need some time to prepare for the next one. We need to schedule passes of the spacecraft over our tracking stations (see Note 1 below), which provide our flight dynamics team the radiometric data they need to determine how well the previous burn performed and to precisely determine the current orbit. They will then prepare the commands for the next apogee-raising burn and, after the commands have been generated, additional passes over the ground stations are required to allow the flight control team to upload the commands. This process repeats until we have executed the final apogee-raising manoeuvre.

Moreover, all the specialists at ESOC (see Note 2 below) have to work fast to perform the apogee-raising sequence of burns with LISA Pathfinder because the spacecraft is passing dangerous terrain on its way out to SEL1: The Van-Allen Radiation belts.

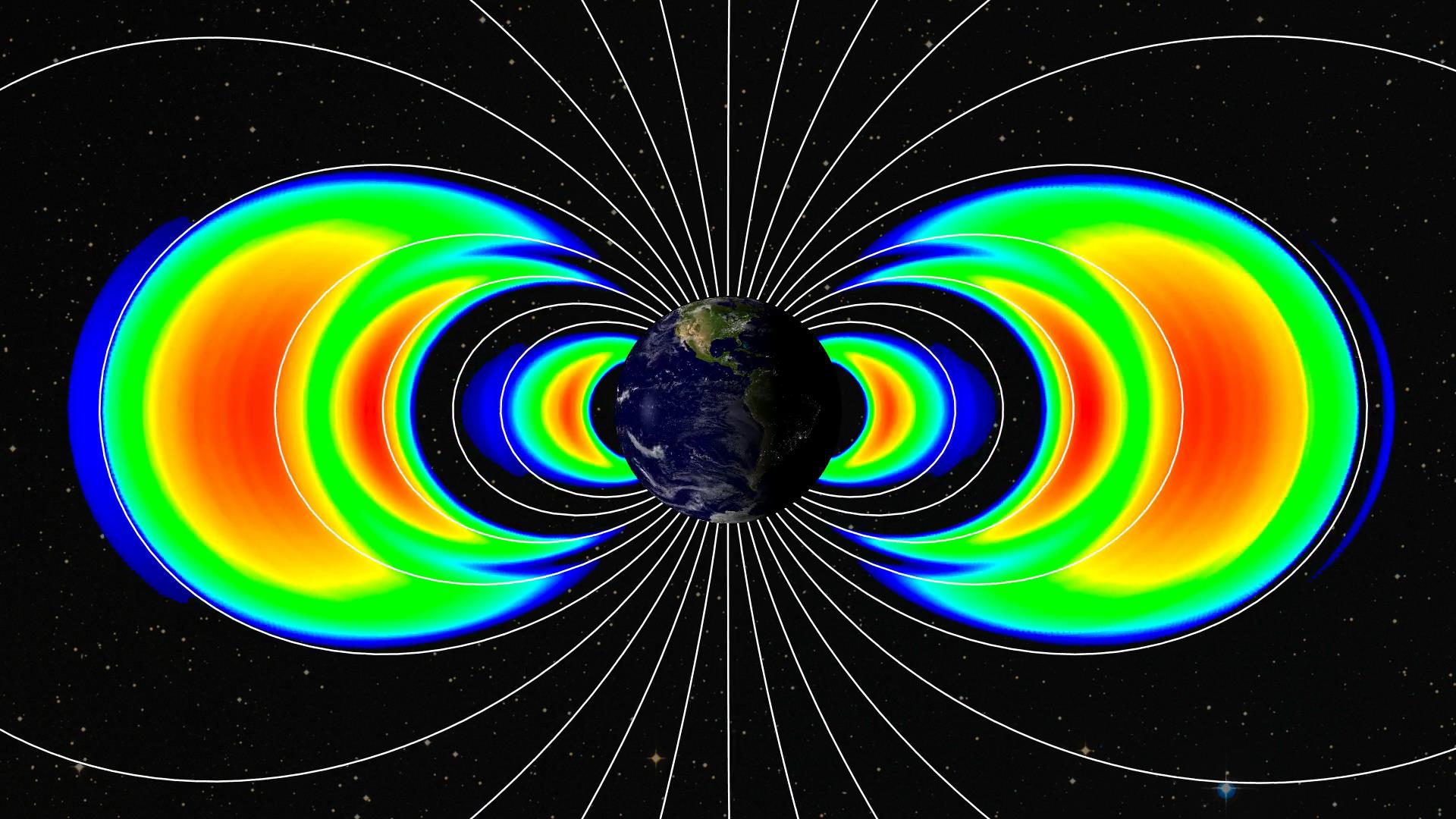
This image was created using data from the Relativistic Electron-Proton Telescopes on NASA's twin Van Allen Probes. It shows the emergence of a new third transient radiation belt. The new belt is seen as the middle orange and red arc of the three seen on each side of the Earth. Image Credit: APL, NASA

This image was created using data from the Relativistic Electron-Proton Telescopes on NASA’s twin Van Allen Probes. It shows the emergence of a new third transient radiation belt. The new belt is seen as the middle orange and red arc of the three seen on each side of the Earth. Image Credit: APL, NASA

These are the reason why the manoeuvres to get to SEL1 are being executed as quickly after each other as possible: We want to limit the time the spacecraft spends in the radiation belts (so as to limit any deleterious effect on the craft’s delicate electronics). It is also the reason why the manoeuvres to propel LPF toward SEL1 are not only optimised for fuel usage and burn duration, but also to limit the time spent in the zones where we expect the highest radiation to occur. For example, the fourth manoeuvre is particularly large, ‘jumping’ over one of the worst zones of the radiation belts.

LISA Pathfinder apogee-raising orbits, prior to departure for SEL1 Credit: ESA

LISA Pathfinder apogee-raising orbits, prior to departure for SEL1 Credit: ESA

Why Vega launched at 04:04:00 GMT on 3 December and no other

The time from lift-off to the time of the final apogee-raising manoeuvre is about nine days, and this time period actually determined the lift-off time of Vega from Europe’s spaceport in Kourou. To put it simply, the lift-off time must be a time such that:

  • After this time, the line of apses (the line connecting the perigee and the apogee) must be oriented such that the final burn following the sequence will actually point the apogee toward the Sun, since we want to fly to SEL1, which is located toward the Sun
  • Vega doesn’t know where the Sun is (it’s just a rocket). No matter what lift-off time, it always flies the same trajectory with respect to the Earth’s surface. However, the Earth is rotating and thus the time Vega leaves its launch pad determines the position of the apogee and perigee with respect to the Sun

So, it fell to ESA’s Mission Analysis team to determine the time at which Vega optimally roared into space such that after nine days the line of apses will be oriented such that we can go to SEL1 and that we don’t fly in the opposite direction (for that we’d launch about 12 hours later). Actually, the lift-off time was calculated such that even in case of delay or other contingencies during the immediate post-launch days (LEOP – the critical Launch and Early Orbit Phase) a correct orbit about SEL1 can still be reached.

In addition, the launch time and trajectory were carefully planned so that LISA Pathfinder stays well clear of the orbit of the International Space Station.

Note that we didn’t have to exactly point toward the Sun to go into an orbit about SEL1, despite this point being located on the direct line between Earth and Sun. There is a certain range where this line-of-apses can point. Nonetheless, there are many other considerations that require us to pick only one specific lift-off time. For example, we want to ensure that the resulting orbit about SEL1 is optimal for communication with the Earth.

LISA Pathfinder orbits to SEL1 Credit: ESA

LISA Pathfinder orbits to SEL1 Credit: ESA

Once the spacecraft starts travelling on the trajectory towards SEL1, another difficult task must be accomplished by the flight dynamics and flight control teams. This relates to the fact that, despite what you always hear, libration point orbits are, unfortunately, unstable and the smallest perturbation can cause the spacecraft either to fall back toward Earth or escape into the inner Solar System.

Keeping our spacecraft up there

Thus, keeping LISA Pathfinder in its orbit about SEL1 is like balancing a pencil on its tip – except it’s actually much more complicated than this because we can only thrust in the Sun direction (due to the design of the spacecraft) and we have very little thrust available on the spacecraft (using just its cold-gas control thrusters) after the science module has discarded the propulsion module.

So, we have to keep LISA Pathfinder in a very delicate balance: the craft must be kept in an orbit that is constantly ‘falling back’ toward Earth, with just very small puffs of gas to push it ‘back up’.

Every week that LPF is at L1, we will have to give it a small push (these are the so-called ‘station-keeping manoeuvres’) so that it doesn’t actually fall back toward Earth. But the push must be small enough so that we don’t fall into the Sun direction either, because then the flight control team would have to conduct a rather complex manoeuvre, rotating the spacecraft so that thrust can be provided toward Earth to get the spacecraft back toward the ‘Earth-falling’ side — and this would make us lose valuable science time.

Once en route to SEL1, a series of six thruster burns will ensure that we’ll end up in exactly the right trajectory – not falling toward the Sun and not too quickly falling back toward Earth either.

This is post highlights just a few of the factors related to trajectory is only a small part of what makes LISA Pathfinder such a challenging – and fantastic! – mission for all teams working at ESOC.

Notes:

  1. Initially, LPF is using ESA’s 15m tracking stations in Perth, Australia, Maspalomas, Spain, and Kourou, French Guiana. Once it is more than about 50 000 from Earth, it will use the three 35m deep-space tracking stations in Spain, Australia and Argentina. Read more about ESA’s Estrack network.
  2. LPF is operated from ESA’s European Space Operations Centre, Darmstadt, Germany, where not only are the Flight Control Team located, but also the extended functional teams of experts in areas like flight dynamics, mission analysis, ground stations and software systems.