
Konstantin Tsiolkovsky (1857-1935) was a high school math teacher and inspired great rocket scientists like Wernher von Braun and Sergey Korolyov (source: Wikipedia).
If there is a man who is at the heart of rocket science, it is Konstantin Tsiolkovsky. The man has quite an unusual professional background, which is not surprising given the fact that in the late 19th or early 20th century space exploration was more a subject of fiction literature (a prominent writer of which was Jules Verne, who deeply influenced Tsiolkovsky) than reality.
It was said of Tsiolkovsky that he was a bit eccentric but withdrawn. He did not excel in his studies as a young man, but the fascination of the possibilities of space travel kept him working in the field. In the early 20th century he taught math in high school. His scientific and technical work covers a broad range of disciplines, from control and propulsion of flying machines to dirigibles and civil engineering. His ambition apparently was to make a contribution so that future generations could enjoy an adventurous and fruitful life in a technically advanced society.
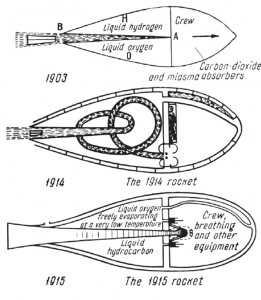
Tsiolkovsky’s drawing of the evolution of a rocket shows his systematic thinking. He has not only considered the propulsion system, but also how the propulsion system would go together with other elements of the vehicle (source: Museum of Flight, Seattle, USA https://www.museumofflight.org)
Tsiolkovsky’s biggest technical contribution is what he called the “formula of aviation,” a formula for the increase in velocity due to a recoil engine (today we call a rocket engine, because rockets are almost the only application of recoil engines).
Tsiolkovsky simply applied Newton’s law to a gas expelled from a nozzle. Written in math this looks like this:
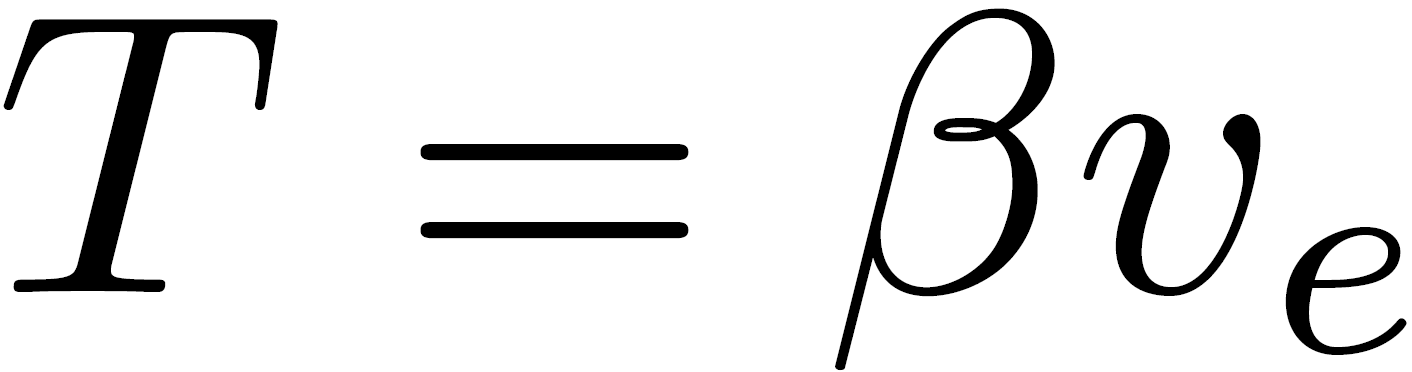
where T stands for thrust (measured in units of Newton), β for the mass flow (measured in kg s-1), and ve stands for the velocity of the exhaust gas (measured in ms-1). The velocity ve can range from a few thousand to millions of metres per second, depending on the propulsion system used, but that’s for a future blog post.
Because the thrust is also the force that propels the vehicle with an initial mass M that loses mass at the given rate β, we can form a recursive equation, that is commonly referred to as a differential equation:
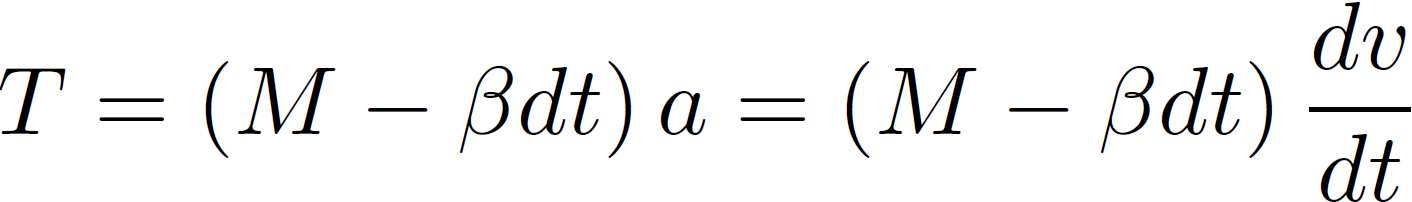
where dt is an infinitesimally small time interval, a is the acceleration (measured in ms-2), and dv is an infinitesimally change in velocity.
Expanding the terms and exploiting the fact that the product of two infinitesimal quantities equals zero, we can derive
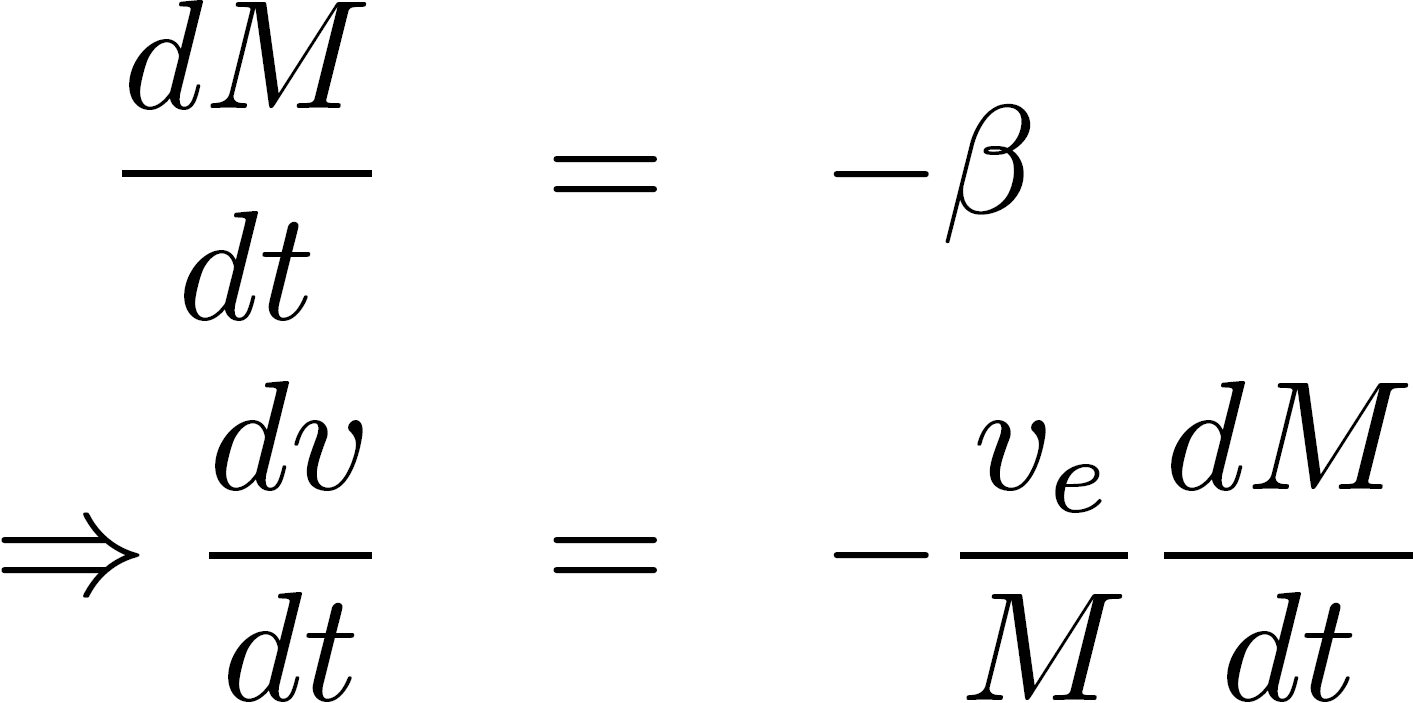
which should hold for any time interval dt. We thus have:
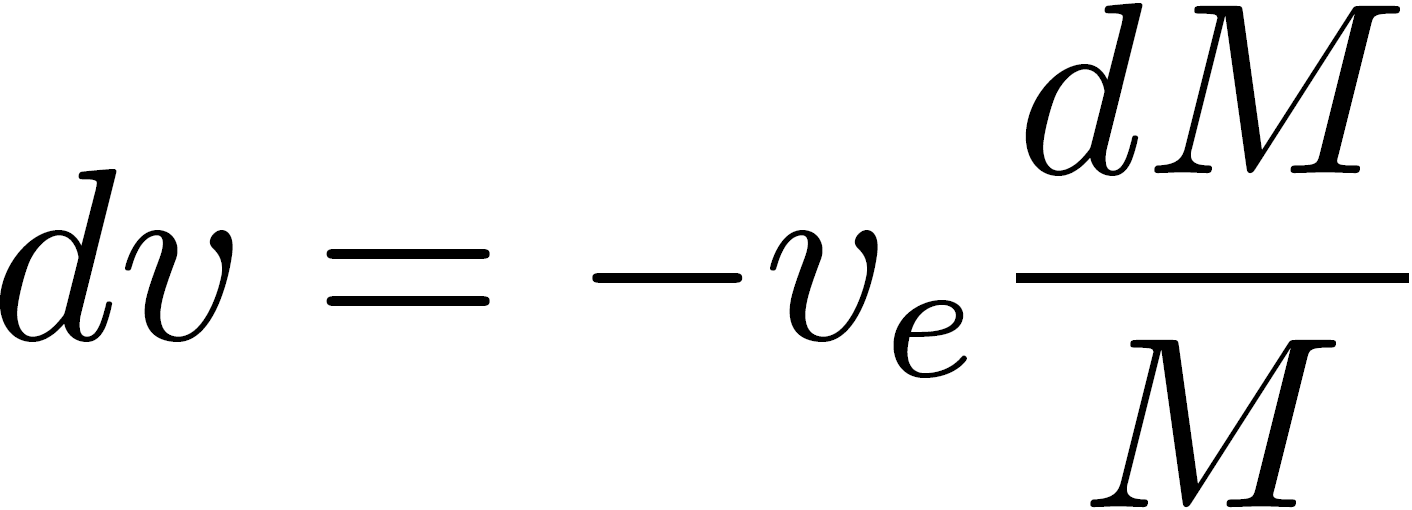
allowing us to find the velocity v(t) after a given time t spent thrusting by application of the rules of infinitesimal calculus that have been found by Gauss and Newton:
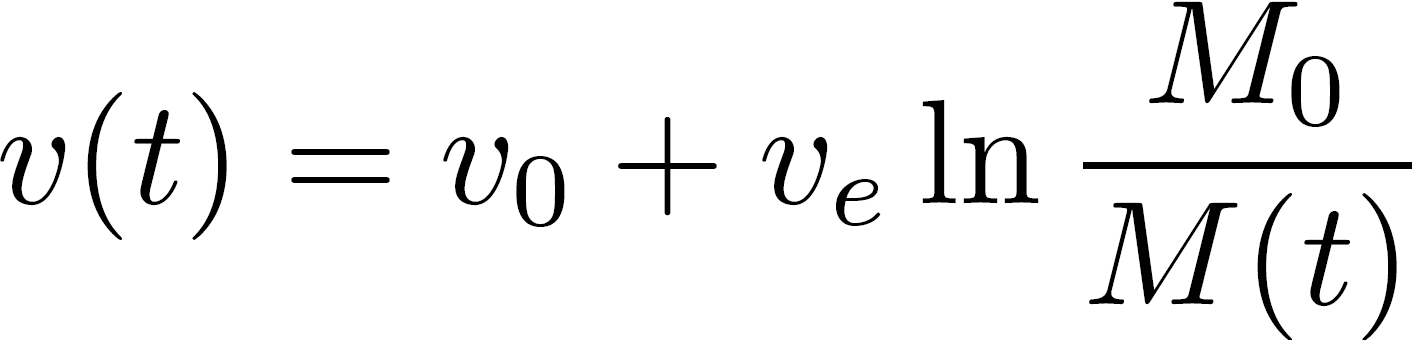
where v0 is the initial velocity (can be zero), M0 the initial mass (that is, the vehicle mass plus all the propellant on board) and M(t) the mass after time t.
This is what we know today as Tsiolkovsky’s Equation. In real applications, it is not the final wisdom with respect to rockets, but it is the basis of everything. If you have to calculate the mass mp of propellent used by a satellite when it changes its velocity by an amount Δv, you can use its inverted form directly:
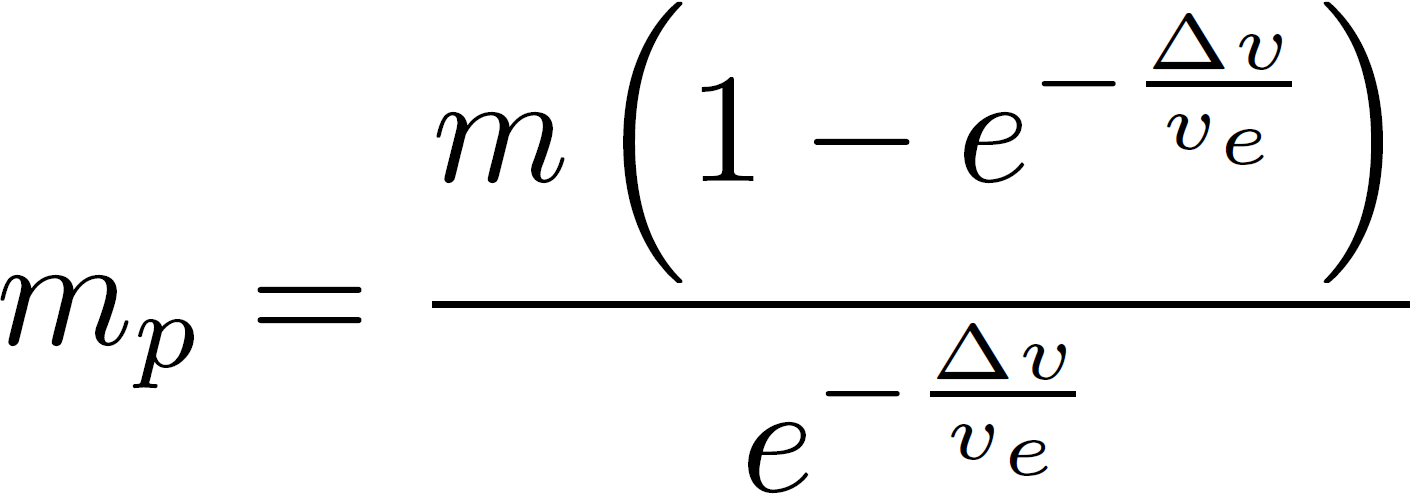
where m is the mass of the satellite (which must be much bigger than the small amount of propellant used for the manoeuvre).
The beauty of the Tsiolkovsky equation is that is uses simple 18th-century physics and math and is highly relevant even in 21st-century space mission design.
Another great achievement of Konstantin Tsiolkovsky, which was probably unintended by him, is that he inspired the great minds of the early 20th century, Robert Goddard and Hermann Oberth. These pioneers were soem of the first to seriously design rockets. That’s why Tsiolkovsky is also called the grandfather of rocketry.
After the terrible wars of the 20th century, it was time for space flight to really take off. On the basis of Tsiolkovsky’s, Oberth’s, and Goddard’s work, the inventor-engineers Wernher von Braun and Sergey Korolyov turned Tsiolkovsky’s dreams into a reality in the mid-20th-century space race.
Another creation of Tsiolkovsky is perhaps not so well known (because you can’t use it as well in military combat as a rocket): when Tsiolkovsky went to the World Exhibition in Paris in 1895, he marvelled at the Eiffel tower and wondered what would happen if it was built so high that at its tip the centrifugal force equals gravity. Thus, he is also the grandfather of the space elevator, but that’s a future blog post!


Discussion: 2 comments
Hi,
thank’s for this nice blog, but is it only me not seeing the formulas?
Looking forward to new blog posts!
Michael
HI Michael: Fixing this now… hang on a mo’!