Editor’s note: Today’s post was contributed by Markus Landgraf from the Mission Analysis Section at ESA’s ESOC establishment, Darmstadt, Germany. It highlights the detailed assessment of options, scientific and practical factors that must be taken into account before any mission can be flown.
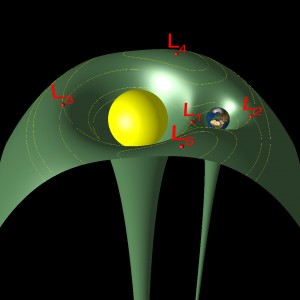
The surface indicates the effective potential created by the two massive bodies and the rotation of the secondary body around the primary. The libration points are located at the saddle points. Due to the non-conservative nature of the potential, no statements of the stability of the libration points can be made from this picture.
If we are to explore not only our solar system, but also the cosmos in more general, we have to rely on telescopes to collect starlight. For most applications this is most efficiently done outside the Earth’s atmosphere and thus follows the need for installation and operation of space telescopes.
Globally speaking Europe leads astronomy research, not only due to our history, but also due to the missions currently in operation: Herschel/Planck, XMM-Newton and Integral. This has been recognized by the Association Aéronautique et Astronautique de France, which awarded the prize for outstanding space endeavours to the Herschel/Planck mission.
The first generation of space telescopes, represented by Hubble, was about exploiting the improved ‘seeing’, that is the excellent angular resolution and spectral stability of the exposures. The second generation, which is operational today, covers the full range of the electro-magnetic spectrum from microwaves (COBE/Planck) to gamma rays (Compton/Integral). The third generation, now in the study phase (in Europe: Cosmic Vision) will see instruments dedicated to more specific tasks: mapping the extra-galactic sky in near-IR or staring at hundreds of thousands of stars for years in the optical band of the electromagnetic spectrum.
All of those missions share a set of basic requirements: maximum accessible sky area, meaning no bright objects distributed over the sky; high thermal stability; low radiation exposure due to sensitive instrumentation; ideally no eclipses of the Sun by the Earth or the Moon; and, fixed Sun-spacecraft-Earth geometry.
How can those requirements be implemented in current missions?
Near Earth orbits cannot be used for highly specialised and sensitive space telescopes mainly because in these orbits the spacecraft can come between the Earth and the Sun, where they receive thermal radiation from two different sides. This means that the large thermal flux makes it extremely difficult to reach low temperatures or to achieve a certain required thermal stability, important for the spacecraft’s payload.
XMM-Newton and Integral are two science missions that have highly eccentric orbits. These orbits were chosen so that their instruments can avoid the effects of the Earth’s radiation belts. However, effects of solar radiation can still be significant for this type of orbit. On a highly eccentric orbit, the time spent at the apogee is much longer than on the remaining parts of the orbit. The apogee passage is, therefore, used for making observations. The higher the apogee, the longer the time available for making observations in a thermally stable environment.

This artist’s view shows the Planck satellite and a sketch of the microwave radiation being collected and focussed by the telescope’s primary and secondary mirrors.
The radiation is then conveyed to the focal planes of the two instruments (LFI Low Frequency Instrument and the HFI High Frequency Instrument). LFI is designed to convert the lower energy microwaves into electrical voltages, rather like a transistor radio. HFI works by converting the higher energy microwaves to heat, which is then measured by a tiny electrical thermometer.
Highly eccentric orbits are Earth orbits within the Earth’s gravitational sphere of influence, where the gravitational attraction of the Earth is greater than that of the Sun. This comprises a two-body system, in which the two bodies are the Earth and the spacecraft, and the remaining bodies of our Solar System are considered perturbing bodies. Once the spacecraft reaches the boundary of the Earth’s gravitational sphere of influence, a three-body system has to be considered (Earth, Sun and spacecraft) and it is within this three-body system that the most suitable orbits for Planck and Euclid can be found.
The two-body problem is characterised by the Kepler potential, that is the gravitational potential of a single point mass. In this potential, there are no points of stability or equilibrium. In the three-body problem there are three forces at work: the gravitational attraction of the two major bodies (in our example, the Sun and the Earth), and the centrifugal force of the secondary body on a circular orbit around the primary body. The effective potential of this circular restricted three-body problem shows points of equilibrium, the so-called Lagrange or libration points.
Libration points in the Earth-Sun system are points in space such that an object placed at one of them will remain there indefinitely relative to that system. In other words, the gravitational force from the Sun, from the Earth and the centrifugal force of the rotation of the Earth around the Sun are balanced. There are five aptly named points: L1, L2, L3, L4 and L5, and they were first discovered by Leonard Euler in 1750, but are named after Joseph Louis Lagrange, whose effort to expand orbital mechanics beyond the two-body problem was notorious.
The Earth-Sun system is not the only system where Lagrange points can be found. In fact, the nearest possible far-Earth orbits around Lagrange points are in the Earth-Moon system. In the Planck mission, these orbits were considered unsuitable, because either the Earth or the Moon is often not very far from the telescope line-of-sight. Simulations showed that, for an orbit in this system, the poor thermal or stray light conditions would affect at least 35% of the data obtained.
With the first missions like SoHo, Herschel, Planck, and – soon – Gaia operating around the Sun-Earth libration points, ESA is starting to accumulate experience in operating on trajectories that are beyond the celestial mechanics of Kepler, but that exploit the properties of the three-body problem: pendulum motion around the points of equilibrium, which are connected to near-Earth space by manifolds that allow manoeuvre-free transfers.
The future of astro- and fundamental physics done in space lies in the exploitation of the benign properties of the libration points, be it in the Sun-Earth or in the Earth-Moon system. The dynamics around these points require a very different kind of mission analysis, with tiny manoeuvres, and high-precision navigation, but offer long times of science operations.
So, if your telescope needs a bit of space, ESA’s Mission Analysis Section is ready to help you find a parking spot 1.5 million km away from home!
Editor’s note: Very nice animation of Planck’s voyage to L2 here.


Discussion: no comments