By Rhett Allain
The primary role of the Automated Transfer Vehicle is to bring supplies to the International Space Station. Supplies include food, water, oxygen, scientific equipment and candy bars. Yes, I listed food twice. Candy is food, but I listed it separately so that we could look at candy in space.
Here is the question: Suppose an astronaut requests an extra candy bar to be sent up on the ATV. How much extra energy is required to get this candy into orbit? That is the question.
Editor’s note: In addition to having a knack for science communication, Rhett Allain is Associate Professor of Physics at Southeastern Louisiana University. He writes regularly for Wired’s Dot Physics blog and is a bit of a physics fanatic who spends more time than many pondering how daily life intersects with science. His recent posts have looked at the physics of a (fake) broken swing image, why doesn’t the Moon crash into Earth (gravity’s involved!), Star Wars blaster speeds (answer: 34.9 m/s) and how well-made are Lego blocks (really well made). With the recently announced development of ATV in cooperation with NASA for Orion, we’re delighted to feature a few posts from the far side of the Atlantic. Enjoy! – DGS
To start, let’s get some initial values. Some of these will be estimates. What about the ISS? It has an orbit that is about 420 km above the surface of the Earth and it moves with a speed of 7,700 m/s. Both the altitude and speed are important in the calculation of the energy needed to get supplies there.

Got the goodies from ATV-2. What, no pizza for me? I guess rehydrated macaroni & cheese will have to do for next few months! Presi i pacchi doni. Cosa? Non c’è pizza per me? Accidenti, dovrò acconterntarmi di pasta reidratata per i prossimi mesi! Credit: ESA/NASA/P. Nespoli
There really is just one other important piece of information. We need the location of the ATV launch pad, which is in Kourou, French Guiana. In case you aren’t familiar with the location, here it is in Google Earth.
Kourou is only 5 degrees above the equator. There is a reason for this as we will soon see.
Oh, we need one more thing. What about the mass of a candy bar? I don’t wish to single out any particular brand of candy, so I will just assume an average chocolate candy bar. Let’s say it has a mass of 50 grams with 250 calories (that’s food calories, which are different than chemistry calories – just to be clear).
Physics and Energy
Now for a little bit of physics. Why does it even take energy to get anything to the ISS? Well, there are two things you need to do to a candy bar in order for an astronaut in space to eat it. First you have to lift the candy up to the height of the ISS. Second, you have to increase the speed of the candy bar so that it is going at the same speed as the ISS. Let me look at these two things separately.
Suppose you find this 50-gram candy bar on the ground and you lift it about 1 meter up to place it on a table. This requires that you do some work on the candy to change its energy. But how much energy would it take? One way to look at this is via the change in gravitational potential energy. On the surface of the Earth, the change in gravitational potential can be calculated as:
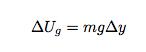 Here, g is the local gravitational constant with a value of 9.8 Newtons/kg. Increasing the height of a candy bar by 1 meter would take 0.49 Joules of energy. That’s not too much.
Here, g is the local gravitational constant with a value of 9.8 Newtons/kg. Increasing the height of a candy bar by 1 meter would take 0.49 Joules of energy. That’s not too much.

How the candy bar gets its kinetic energy: Liftoff of Ariane 5 VA205 with ATV-3 Credit: ESA – S. Corvaja, 2012
Now, what if I want to increase the height of the candy bar all the way up to the ISS? Can I just do the same calculation but change the height from 1 meter to 420 km? No, I can’t. The above model for gravitational potential energy assumes that the gravitational force on the object is constant. This is a good assumption near the surface of the Earth, but not so good as you get higher (though at the ISS height it isn’t the worst approximation you could ever make).
If we use a better model for the change in gravitational potential, it would be this:
Here, G is the universal gravitational constant. The two masses in the expression are the mass of the candy bar and the mass of the Earth. The values on the bottom of the expression are the distances from the centre of the Earth. So, the candy bars ends at the altitude of the ISS (I call this h) and starts at the radius of the Earth.
If you put in the values for G and the radius and mass of the Earth, you would find that it takes 1.93 x 105 Joules of energy to get that candy bar up to the right altitude.
But that’s not all of the energy for the candy bar. If you put that much energy into the candy and let it go, it would just fall back to the Earth. The other kind of energy the candy needs is kinetic, i.e. moving, energy. This has an expression of:
 Since we know the speed of the ISS, shouldn’t this be easy to calculate? If I put in the mass of candy (0.05 kg) and the speed of 7,700 m/s, I get a kinetic energy of 1.48 million Joules. Actually, this is the wrong answer. Why? It assumes that we took that candy and increased its speed starting from rest. The only problem is that before the launch, the candy is already moving. It is moving because it is on a rotating Earth.
Since we know the speed of the ISS, shouldn’t this be easy to calculate? If I put in the mass of candy (0.05 kg) and the speed of 7,700 m/s, I get a kinetic energy of 1.48 million Joules. Actually, this is the wrong answer. Why? It assumes that we took that candy and increased its speed starting from rest. The only problem is that before the launch, the candy is already moving. It is moving because it is on a rotating Earth.
Let’s say the Earth rotates once every 24 hours (which it doesn’t actually – that is the time for the Sun to get back into the same position but this value is close enough for us). This means that the speed of the candy before launch can be calculated as:
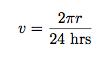 But what is r in this expression? It is the radius of circle in which the object moves due to the rotation of the Earth. At the equator, r is the radius of the Earth. At the North pole, the radius would be zero. If I put in the radius of the Earth (and convert hours to seconds), I get a starting candy bar speed of 464 m/s. That might be small compared to the ISS speed, but every little bit helps. And this is why ESA launches the ATV from Kourou. It is very close to the equator.
But what is r in this expression? It is the radius of circle in which the object moves due to the rotation of the Earth. At the equator, r is the radius of the Earth. At the North pole, the radius would be zero. If I put in the radius of the Earth (and convert hours to seconds), I get a starting candy bar speed of 464 m/s. That might be small compared to the ISS speed, but every little bit helps. And this is why ESA launches the ATV from Kourou. It is very close to the equator.
OK, so what about the new change in kinetic energy of the candy? Launching from the equator, you would need about 1.47 million Joules.
The total energy to get this candy bar to the ISS is just the sum of the two values we’ve now calculated: the change in kinetic and change in gravitational potential energy. This works out to 1.66 million Joules. That is over a million Joules of energy for just that one tiny candy bar and it assumes a perfectly efficient method for getting things into orbit without any energy losses. This is why we don’t all live in space. It’s just expensive.
Energy to orbit using candy
It’s pretty hard to get a feeling for an energy of 1 million Joules. What about a comparison to the energy in the candy bar? If you consume this candy, it can produce 250 food calories. One food calorie is 1000 calories which is 4,180 Joules.
Let’s go backwards. If it takes 1.66 million Joules to get candy into orbit, how many food calories is that? This is a pretty straight-forward unit conversion problem. Remember that the trick to unit conversions is to always multiply by a fraction that is equivalent to 1.
Well, that’s not so bad. It takes a little more than 1 candy bar of energy to get a candy bar to the ISS!
OK, one more thing: What if we wanted to get all of the ATV cargo to the ISS just using candy as energy? The ATV can carry a payload of about 20 tonnes, or 20,000 kilograms. If this payload comprised just candy bars, that would be 400 thousand bars of candy; the energy needed to get into orbit is the same energy you would get from consuming 640,000 candy bars.


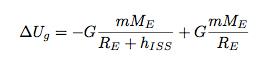

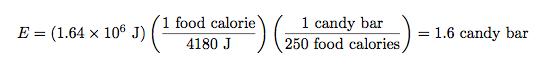
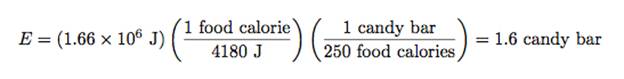
 Automated Transfer Vehicle page
Automated Transfer Vehicle page ATV blog archive
ATV blog archive
 NASA Orion page
NASA Orion page NASA Artemis
NASA Artemis Airbus Orion page
Airbus Orion page
Discussion: 18 comments
It’s a really interesting question, and fairly nicely answered.
A few points:
“at the North Pole, the radius would be zero” – n0.
“At the equator, r is the radius of the Earth” – r varies with latitude and longitude. However you might have just assumed that Earth was a sphere. From a physics standpoint, we might need to look back over our polar coordinates.
The 100% propulsive efficiency is a bit tentative. I bet it’s incredibly low, heating up a hell of a lot of air on the way up.
Another thing you missed was that we don’t absorb all of the food calories we consume, and not all of what is absorbed is goes onto producing useful work.
@Jay,
When I say the radius would be zero at the North Pole, I mean the radius of the circle the object is moving in due to the rotation of the Earth. If you were standing at the North Pole, you wouldn’t really be moving in a circle, you would just be spinning around where you stand. Also, you would be very cold.
Yes, there would be lots of energy lost to heat also during the launch.
I was just curious, does this energy calculation is assume at the initial time, the space station is directly above the launch point? Also does the rotation around the sun and other rotations (galactic ect.) come into play with the actual energy needed? Also where does that derivation for the delta potential energy come from with the varying gravitational force (calc is a bit rusty if you have a helpful link that would be fine 😉
@Warren,
Of course real orbital mechanics can be quite a bit more complicated. However, the amount of energy needed to move around in the same orbital space is much smaller than the energy needed to get there.
There was no assumption about where the station is in reference to the candy bar, when you launched the candy bar. That would require knowing how long you will accelerate the candy bar. For instance, did you try to launch the candy bar with a directed explosion or a long and controlled propulsion.
Other energies like earths rotation around sun or solar systems rotation around the milky way do not come into play here because… Lets start with earth’s rotation around sun. The ISS and the earth share eventually the same reference frame in the context of rotation around the sun. A similar answer exist for rotation around the milky way galaxy, and the milky way’s orbit in the local cluster of galaxies. On the other hand, if you wanted to launch the candy bar to the Andromeda galaxy, you would need to factor in each of the rotations.
Hi,
Thanks for the interesting calculations ! Now I’ll be able to lecture my 4 years old on how not everybody is lucky enough to get candies (I’ll skip on the fact that’s because they’re on the ISS).
Just a question, though, if I’m not mistaken, your delta-v calculation seem to imply that the ISS orbit is parallel to the earth rotation direction? But as far as I know, that’s not the case. Is your approximation close enough or did you not know to drown us in math ? 🙂
Thanks!
@Colin,
Yes, I did assume the ISS orbit was in the same direction as the rotation of the Earth. This isn’t quite true – but how did the ISS get there in the first place? It was also launched from Earth (in pieces). So, most stuff in low Earth orbit generally orbits the same way.
To launch from earth’s equator to a retro orbit would require even mo4e energy.
Hi,
Thank you for your reply 🙂
Correction, “did you not want to drown us in math”, of course.
But when the rocket goes up wouldnt that speed add up for the direction to the ISS? So less kinetic energy might be required?
I can imagine also that it might be more efficient if the rocked would fly in a curve more rounded at the top
@Peter,
Well, if you want to dock with the ISS (how else could you get your candy), you have to have the same orbital speed that the ISS has.
Energy to go strait up is different than the energy to achieve orbit for the same altitude.
Well, not that simple. Of course, you can put the candy bar into a cannon and supply all the required energy at once, calculating the ballistics so that the bar will reach the ISS with the exact speed. In reality, the energy to the candy bar is supplied all along the trajectory. In this case, you need to take into account the mechanism of the energy delivery. The latter itself require spending energy, a lot of it. All this may increase your estimate of 1.6 by several orders.
The tyranny of rockets. Given the real world premise, delivery method matters, and the proposed question implied the morsel is included as extra cargo on flight to ISS. Assuming one wishes to avoid the possibility of nuclear calamity, burning hydrogen provides the strongest energy/mass propulsion ratio. Using hydrogen/oxygen, the mass fraction (of total rocket mass) for propellant to launch to near earth orbit is 83%. This does not include efficiency losses, including atmospheric drag and incomplete combustion. Space Shuttles were ~ 85% propellant by mass. Soyuz re-supply rockets burn kerosene/oxygen, and are about 90% fuel at launch mass. Most of the energy cost for the trip (dominated by the orbital acceleration) is spent in the early phase of ascent in dragging along the fuel needed to reach the target. Thus, one needs about 10-20 wt-equivalents of fuel to deliver each delicious morsel, depending on fuel choices.
e.g., https://www.nasa.gov/mission_pages/station/expeditions/expedition30/tryanny.html
Very illustrative thought experiment. The tangential comments drifting into the practical aspects of achieving orbital energies have been both insightful and incorrect. One notable mistake is that the candy bar, by itself, has very little available energy. One must supply an oxidizer to liberate the chemical energy contained. Assuming that the candy bar, being mostly made of hydrocarbons (fats and oils), burned with oxygen, would require about the same mass mixture ratio of a hydrocarbon rocket engine, about 2.6:1. So along with the 50 grams of chocolate bar another 130 grams of oxygen is needed. This doesn’t change the premise of the original article; the energy is unchanged. In the reality of rocketry however, this means that you have to accelerate the oxygen, along with the chocolate bar fuel, until it is burned and ejected out the exhaust. This is one of the real losses inherent with the process. Even so, rocket systems are still the most efficient means of accelerating things we know of.
Wow! You are so awesome. Explain in detail about the calculation and everything.
Thank you for this very useful article.
So how many gallons would it take to get me to the ISS?
——————————————————————————–
If it takes 1.66 million Joules to get a 50 gram candy bar to the ISS, and I’m 100 kg, then doesn’t it follow that:
– there are 20 * 50 g in a kilogram,
– there are 100 kilos on a hundred kg,
hence the energy required to get me to the ISS would be 1.66 million * 20 * 100
which equals: 3320000000 Joules
BUT how many Joules are there in a gallon of petrol?
1 Gallon of Gas = 120,276,384 Joules
So how many gallons would it take to get me to the ISS?
3320000000 / 120,276,384 = 27.6 Gallons.
Somehow, this doesn’t seem right! Of course, I’d have to add the weight of the gas, but do you7 see where I’m going? Not to the ISS, it would seem!